5. Effect of material conductivity
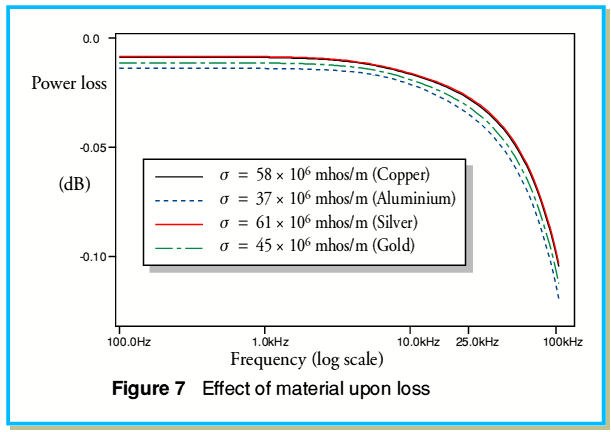
We can now examine the effect of various choices of conductive material. Figure 7 illustrates the effect of using four different choices of metal for the wires. The same wire diameter and spacing is assumed as previously, and the fill factor is assumed to be unity.
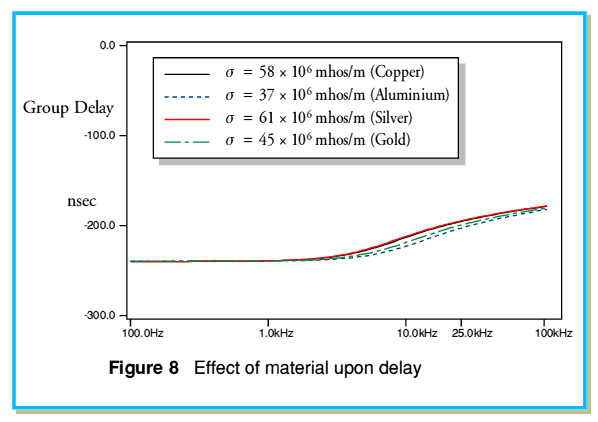
Figure 8 shows the related results for signal delay values.
As with variations in fill factor, the variations between the materials used as examples here seem quite small. Hence it is not obvious that changing, say, from copper wires to silver ones of the same diameter and spacing is likely to produce an audible change as a result of differences in the internal impedance of the wires. Curiously, although aluminium is generally regarded as a ‘poor’ choice for wiring in audio systems, its relatively low conductivity does mean that the effects of internal impedance tend to occur at slightly higher frequencies than copper.
It is interesting to note that the nominal behaviours of copper and silver are quite similar compared to their difference from aluminium or gold. However it is worth bearing in mind that most of the metals used for wires are far from being of elemental purity. This means that the actual conductivity of a wire may differ by perhaps 5% or more from the standard values assumed for the above calculations. This in itself is unlikely to be significant compared to the much larger range in conductivities for the materials used here as examples.
6. Effect of low conductivity material
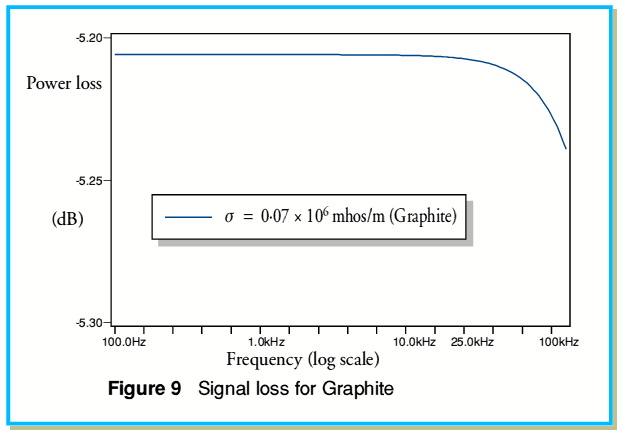
Having noticed the effect of the relatively low conductivity of aluminium some manufacturers and writers have argued that it would be better to deliberately use a material with a particularly low conductivity. Carbon (graphite) has frequently been mentioned in this context. To estimate the effect of using such a material we can now use figures 9 and 10. These show the relative loss and phase delay for the two materials and our standard example of cable.
Figure 9 shows a result which at first examination seems strange. The graphite has a conductivity around three orders of magnitude lower than that of copper. The skin depth in graphite at any frequency is therefore around 30 times greater. For a given wire diameter this might lead us to expect any increase in loss as the frequency rises to be shifted up to much higher frequencies in graphite than in copper. Yet figure 9 does not seem to show this. The increase in signal loss at 100kHz is around 0·05dB greater than the loss at d.c. This is lower than the the drop of around 0·1dB we would obtain using materials like copper, but the improvement is surprisingly small given the factor of 1000 in conductivity.
To understand this behaviour we can consider an example where we have two rods of material which have the same diameters and lengths. One material has a conductivity which is 100 times lower than the other. As a result the end-to-end d.c. resistances of the rods also differ by a factor of 100. The frequencies at which the a.c. resistances of the rods double due to the effects of finite skin depth (internal impedance) also differ by a factor of 100. We can now define a specific value of the ratio of skin depth to diameter (and hence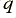 
) which is the value for which the a.c. resistance is double the d.c. resistance. For the rod of lower conductivity material this value of 
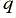occurs at a frequency 100 times higher than for the rod of higher conductivity material.
As a result of the above we would expect the effect of skin effect to be shifted up in frequency by a factor of 100 when we change from the higher to the lower conductivity rod. However, we must then also take into account another difference which turns out to be significant. From the above we can say that the higher conductivity rod can be said to have a d.c. resistance, 
, which increases to 
at a frequency we can label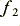 
. The lower conductivity rod will have a d.c. resistance of 
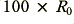which rises to 
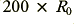at a frequency 
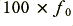. Another way of looking at what happens is therefore that the higher conductivity rod changes its resistance by an amount 
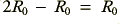when we change the frequency by an amount 
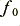. Whereas the lower conductivity rod changes resistance by 
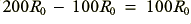when we change the frequency by 
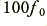. This means that in each case the overall rate of change of resistance as we change the frequency will be
i.e the same in both cases!
This example is not exact and the behaviour is more complex than described here. However this example shows why it turns out that both materials show a noticeable change in signal loss at much the same frequency. Hence for a given wire diameter changing the choice of material has much less effect upon the frequency dependence of the signal loss than we might expect. In fact, we have already seen this to a lesser extent. If we examine the earlier results for fill factor we can see that the main effect of a fill factor of less than unity is to displace the loss curve to a higher or lower overall loss, not to changes its shape.
Using the same wire diameter, etc, as before, do see a marked increase in the low frequency loss due to the lower conductivity. This is simply due to the wires having a much higher d.c. resistance when we change to a material like graphite which has a relatively low conductivity. In practice the level of loss in the example chosen here (around -5 dB) would be far too high for a loudspeaker cable. When using such a lower conductivity material we would therefore probably choose to employ wires of much greater diameter (and hence cross-sectional area) to ensure a low level of loss. However it should be noted that this will mean a change in the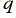 
value at any given frequency and alter the cable’s behaviour in other ways.
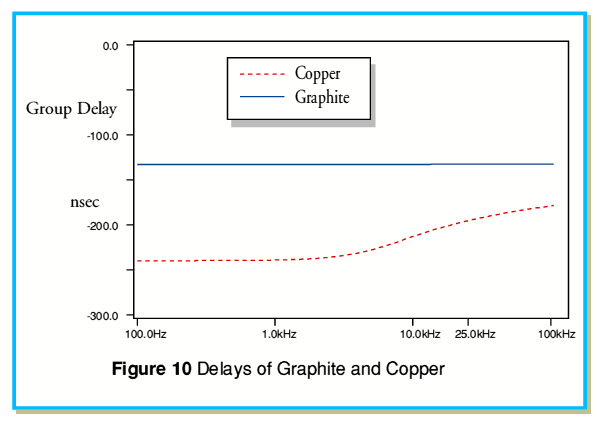
Figure 10 shows the phase delay behaviour of graphite and copper. In this case the behaviours of the two materials are clearly very different. At low frequencies the inductance of the wires is not dependent upon the resistance level. Hence we do not see the ‘scaling’ effect we encountered when looking at signal losses which there tends to offset the reduction in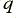 
at any frequency produced by the lower conductivity. From figure 10 therefore we can say that the variation in phase delay with frequency in the audio band is much smaller with graphite than with copper. The graphite also shows a lower overall delay as well as better uniformity. Hence low conductivity materials may be useful if we wish to reduce differential phase/time effects.
However we must draw such a deduction with care for three reasons.
- Firstly, the phase changes at audio frequency are very small, even using copper. It is therefore questionable that they would be audible.
- Secondly, the above assumes we have maintained the diameter of the wire when changing to a lower conductivity material. As we can see from figure 9 this would produce quite high signal losses, and would make the response more sensitive to any frequency dependence of the load impedance.
- Thirdly, we can interpret the reduction in the dependence of the delay upon frequency as being due to the relatively high cable resistance ‘swamping’ the inductance. i.e. the wire resistance is now so high that the cable/load system begins to look more like a simple resistive potential divider with a relatively negligable inductance.
In practice we would probably choose to increase the wire diameter to keep down the overall level of wire resistance. This increase in wire diameter would also increase the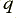 
value at any frequency, thus lowering the frequency at which phase changes may occur.
