The Long and the Short of it!
In conventional information theory terms, it is an axiom that if two signals have essentially identical power spectra and essentially identical phase spectra, then they are indistinguishable and carry the same information. Indeed, identical amplitude and phase spectra imply identical waveforms of signal level variation in time. On this basis, if we assume that nothing above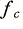 
is audible,
then waveforms whose amplitude and phase spectra up to this frequency are the same should sound identical. Hence it may be concluded that a low-pass filter that does not change the observed spectrum in the audible range cannot possibly have an audible effect.
However a possible problem with the above argument is that we may be making the wrong choices for the way we are working out the spectra, and hence obtaining results that are misleading when considering for human perception. The relevant factor that I am focussing on here is the choice of the chunk of time during which the spectrum is assessed. However there are also some other factors which I will not deal with in detail here.
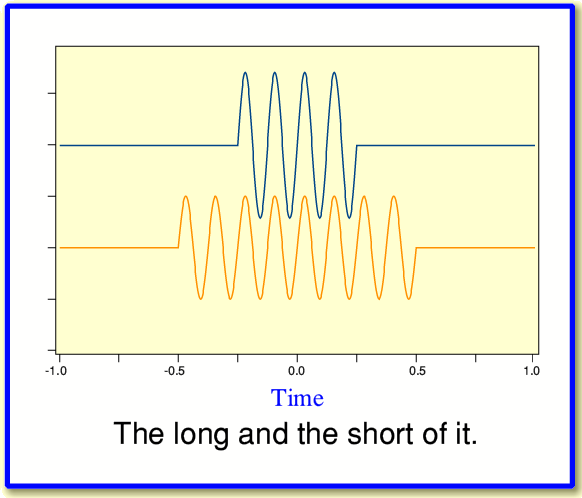
This point can be clarified by using the example shown in the illustration shown below. This shows two sinewave bursts. The share the same sinusoid frequency when ‘on’, but one lasts for longer than the other and is at a lower level whilst it is ‘on’. Their relative timings are arranged so that they both occur in the center of the time period we are examining. As a result, at the chosen toneburst sinewave frequency, we find that – averaged over the period from time = -1 to +1 – they share the same values for power and phase. Yet despite this, one clearly starts before the other, and finishes after it.
In Information Theory terms, we could go on to show that the two waveforms do indeed actually have different power and phase spectra, but that when measured over this time period, these differences only show up at frequencies other than the ‘obvious’ one chosen for the toneburst sinusoid. More relevant here, though, is to note that if we had chosen a different range of times – say from time = 0·25 to 0·5 units – for working out the spectrum, the two waveforms would then have been found to have different powers and phases even at the chosen sinusoid frequency!
When performing a Fourier Transformation to obtain the spectrum of a signal pattern we have to start by choosing the time interval we are interested in. In general, changing this time period will also alter the resulting power and/or phase spectrum. This is part of a more fundamental point which often goes overlooked. Namely that the meaning of terms like ‘frequency’ depends is not unique and unambiguous. Hence when using a method like Fourier Transformation to work out a spectrum we have to take care to ensure we have chosen an appropriate set of circumstances for the process.
The above acts as a warning that we have to apply and interpret spectral methods with great care. Unintentionally choosing an ‘inappropriate’ chunk of time for our analysis might give misleading results in terms of what might be audible, despite the actual calculations being absolutely correct in terms of the relevant information and signal processing theories. The problem here is not with Information Theory or Fourier Transformation, but with how these methods and arguments are applied in a given case.
As a consequence we may have to be cautious about deciding if results obtained by such methods really do tell us what we need to know about pre-ringing! It might, for example, be the case that some of the signal power is now appearing ‘early’ during the pre-ringing, and is being balanced out when we make average measurements by other changes later on in the waveform. The result may then be a filtered waveform whose phase spectrum in the audible range may seem the same as the unfiltered input, but where energy has been redistributed in a symmetric manner about the chosen central instant of the time interval being examined.
