Resolution
We can now take the above technique even further. For the -90dB example we still had a sinewave whose amplitude allowed it to produce changing sampled values even when no noise/dither was added. Let’s now look at what happens when the sinewave which is our original signal is so tiny that it’s wiggles are all confined to one band. For the sake of example, let’s choose a 1 kHz sinewave whose amplitude is -105 dB compared with the CD-A maximum level. This corresponds to an amplitude that only swings over less than half the amount that is required to cover a full quantisation band.
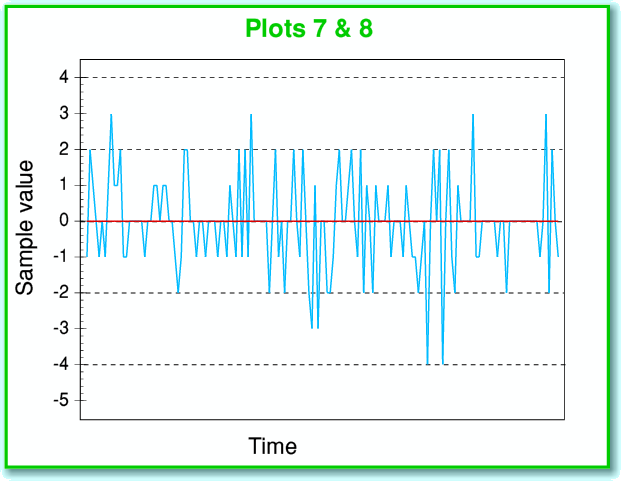
Plots 7 and 8, above, show snippets from the series of sample values that this very low level 1 kHz sinewave produces. The red line shows the series of samples we get if no noise or dither is added to the sinewave before sampling. The blue line shows what we get if we add noise or dither. We can immediately see that – in the absence of any noise/dither – we get no sign of the sinewave at all! Instead we just get a series of identical values. However when we have added noise we can see that we get varying values from one sample to the next. We can’t really see any sinewave in the above, though.
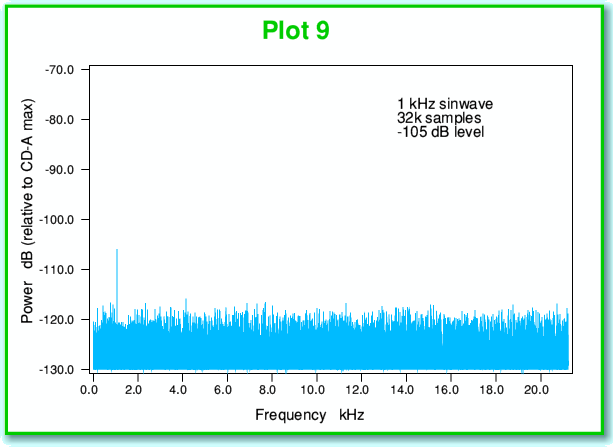
There is no point in computing the spectrum of our noise-free undithered -105dB sinewave as it has zero power at every possible frequency and carries no information or power at all. However the above spectrum (Plot 9) shows what we get from the series of samples where noise was added before sampling. Once again the plot clearly shows the 1 kHz signal standing above the noise background.
In some ways this result looks like magic, but it is possible to show using the formal mathematical methods of Information Theory that this is the result we should expect. Once we have added some suitable noise or dither, our series of samples can record and provide information on signal patterns whose amplitude is smaller than the quantisation interval of the individual sample values.
In fact, Information Theory shows that, in principle, we can record all the information of an input analog signal pattern by a series of digital samples provided we satisfy a set of requirements. One of these requirements is that the quantisation level for the sampling must be smaller than the typical amplitude of the noise. The result when we use the series of samples is the original combination of a signal with some noise. For both the input before sampling, and the output produced by reconstruction of an analog pattern from the samples, our ability to identify or detect details is limited by the noise in exactly the same way. This means that if we sample and reconstruct according to the requirements laid down by Information Theory we should recover a result indistinguishable from the sampled pattern. Dither is the process where we deliberately ensure we have the noise this requires.
The above follows from the work of Shannon and others who founded information and communications theory. Their work also shows that analog signals suffer from precisely the same limitations as correctly sampled and dithered digital systems. In analog systems the natural random noise always limits the level of detail we can find. This stems from the physics of the natural world. Hence it can be formally shown that it is quite incorrect to assume that “analog has an infinite resolution and digital does not,” despite sometimes seeing claims like this in audio magazines or discussions. With both ‘analogue’ and ‘digital’ systems the actual resolution depends upon the noise level, the bandwidth, and the duration over which a signal is observed in essentially the same way. In practice what matters is how well a given system is implemented.
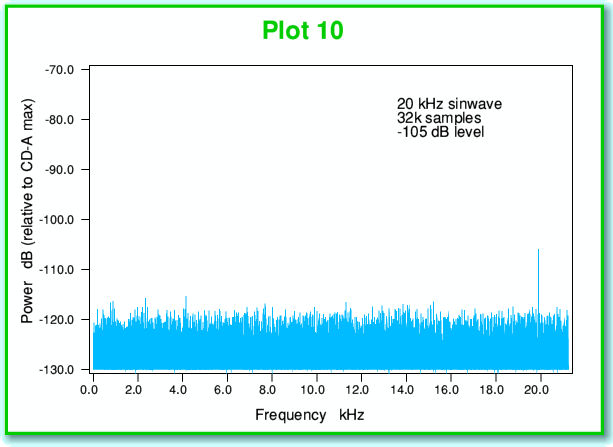
Provided that the noise/dither has suitable characteristics the above result applies equally to any waveform we wish to record and replay. So, for example Plot 10, below, shows the spectrum we get for a -105 dB 20kHz sinewave which was dithered before sampling.
Here I am using sinewaves as examples as these are the most familiar types of simple waveshapes that people use for test purposes. However the relevant parts of Information Theory do not apply only to sinewaves. The results are quite general, and also apply to any other waveshapes that extend across our recorded sequence of sample values. In the context of human hearing, it should be remembered that we do not listen to indivual samples, nor to isolated instantaenous pressure levels. Our hearing responds to patterns of sound pressure variation. Hence human hearing performs processes analogous to the spectral processes employed here. The details differ, but the same basic rules of Information Theory, etc, apply to all physical systems that convey or sense such pattern information.
Page 3 of 4