Some time ago I produced an application that worked out the power-frequency spectrum of a user-chosen section of a sound file. The application is called !TrackTrans and a copy accompanied an earlier article in this series. It worked by the process known as Fourier Transformation. However, if you have used it you will know that the application takes some time to work out the full spectrum. This is because is uses a simple – but slow – method to do the calculation.
The ‘slow’ method has some advantages. For example, it is easy to understand, and to write a computer program which can be studied or modified. However most serious computations of the spectrum of a signal tend to adopt ‘Fast Fourier Transform’ (FFT) methods which – as the name indicates – are much quicker. So I decided it was about time I produced such a ‘fast’ application, which I have duly now done, and have named !TrackFFT. A copy of this should be available in the usual manner, and you can make use of it as you wish.
The way you set up and use this new application is essentially the same as for !TrackTrans, so I won’t repeat the previous explanations of how to do this. If you wish to find out, the information is in a Help file inside the applications, and has been described in previous articles. What I will do is to discuss the main differences in use between the FFT and slow transforms and the effects they have on the results you get.
!TrackTrans loads a chunk of sound data that contained 2205 samples for each stereo channel. This corresponds to 50 milliseconds for CD Audio data. However !TrackFFT loads 8192 samples per channel, corresponding to just over 180 milliseconds of audio. This is because FFTs generally have to operate with numbers of samples that are an integer power of two. 8192 is 213, so is OK for an FFT, but 2205 won’t fit this requirement. This change has one significant effect on the results. Fourier Transformation to generate a general spectrum works on the basis of choosing a series of frequencies which all have an integer multiple of cycles in the duration of the chosen chunk of samples. For 2205 samples (50 milliseconds) this means the resulting spectrum will be specified in terms of the power levels at dc (zero Hz), 20Hz, 40Hz, 60Hz, 80Hz, etc. i.e. at multiples of 1/50ms. But using 8192 samples per channel we now have a basic frequency of 44100/8192 = 5·3833... Hz. So the frequency components in our spectrum will be at integer multiples of this value. In fact, there are a variety of types of computational method which can be called an FFT, and there are some ways around this problem. But they make an already complicated and hard to understand program even more complicated, and also tend to slow things down. So in general, people just use one of the optimal forms of FFT and accept this tends to lead to awkward frequency scales.
I am not even going to try to explain all the details of how an FFT works as understanding them can be a nightmare! But I will try to outline the basic ‘tricks’ involved. To do this I will also explain the idea behind Fourier analysis. Lets start with the arrangement illustrated in Figure 1.
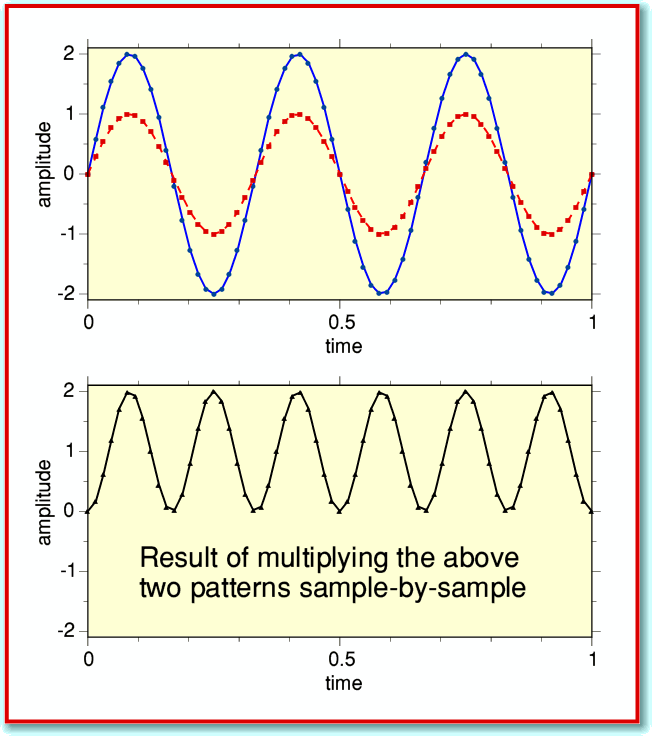
This shows two graphs. The upper graph plots two patterns. The solid (blue) line represents an input signal waveform, and the broken (red) line a ‘test sinewave’ of a chosen frequency. In this case the input signal happens to be a sinusoid of the same frequency and phase as our ‘test sinewave’. The analysis works by multiplying the two patterns together on a sample-by-sample basis and adding up the results of these multiplications. The result in this case is shown by the solid (black) like in the lower graph of Figure 1.
Now in this case the two waveform shapes are the same, although the input signal has a larger amplitude. This means that whenever an input sample is positive, so is the corresponding sample from the test sinusoid, and if one is negative, so is the other. The consequence is that each multiplication produces a positive result (or zero). So if we add all the results from the sample-by-sample multiplications we get a positive result.
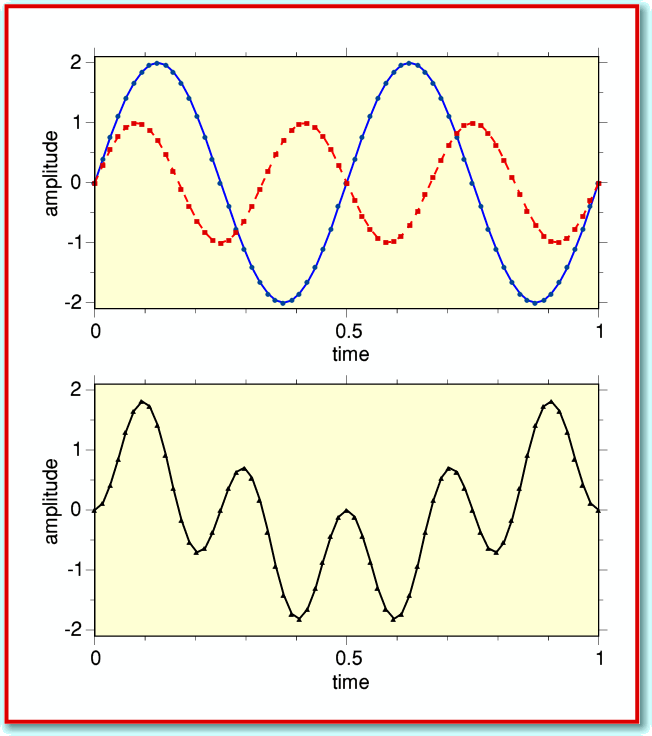
Compare this with the situation shown in Figure 2. Again, the input signal is a sinewave, but it has only two cycles in the time period we are considering whereas our test sinewave has three. Now when do our sample-by-sample multiply we get the result shown in the lower graph of Figure 2. These multiplications produce some negative results as well as positive ones since the input and test patterns no longer always share the same sign. Hence when we add up the results we end up with a small value, or zero.
This process is at the heart of Fourier analysis. In effect, when we add together all the values obtained by the sample-by-sample multiplications we get a result which indicates the level of any variations in the signal which shared the same frequency as our test sinewave. Variations at the ‘correct’ frequency add up to a large result. Variations at other frequencies then to make little or no contribution to the sum of the sample-by-sample multiplications.
This means that when we have some other input signal pattern we can try the above method for various test frequencies. By doing it for various number of cycles in the chosen time period for which we have samples we can determine the effective amount at each frequency contained in the signal pattern. (We also have to do cosines, but the argument is the same.) The results then tell us how much of the signal power presents itself as being as being at each of the tested frequencies. Hence we have worked out a power-frequency spectrum. The problem is that – as described – the process is quite slow when we have many samples to analyse, and lots of possible frequencies - even when we limit the chosen frequencies to just those with an integer number of cycles in the time period covered by our set of signal samples.
Fortunately some tricks have been spotted and can be used to speed up this process quite dramatically! The first is to spot that our test sinewave tends to repeat the same series of values over and over again during each of its cycles. Since multiplications take longer than additions we can then hope to speed things up if we re-arrange the input data to combine signal samples we want to multiply by the same test value before do the multiplication. A similar ‘trick’ is to spot that when we double the frequency of the test sinewave we are essentially just weeding out alternate values and shifting the remaining ones together. This means we can ’rearrange’ all the signal sample information before we do any multiplications, then do just a relatively small number of multiplications, and then unscramble the rearrangement to reveal the spectrum!
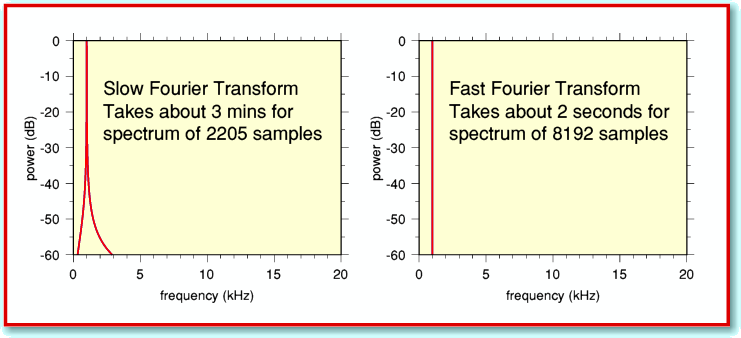
The above is far from being a complete and accurate explanation of how an FFT works, but I hope it gives a flavour of the kinds of mathematical short-cuts used. The consequences can be quite dramatic. To illustrate this, Figure 3 compares the results of using the slow and FFT methods on the same input. Here I have used a sound data file which contained a 0dB level 1 kHz sinewave as the input signal.
The FFT is much faster, and only takes a couple of seconds to work out the spectrum, although the application then takes a few more seconds to list the results in a Taskwindow. (These timings are for my Iyonix, so may vary on other machines.) The spectrum produced by !TrackFFT also has a higher frequency resolution as it uses 8192 samples instead of just 2205. If the slow method had been asked to use as many samples as the FFT it would have taken well over ten minutes to do the job the FFT does in 2 seconds. From this comparison you can see why the FFT is preferred by people who have a lot of data to analyse quickly!
As with the previous example applications in this series !TrackFFT works on the ‘data’ format of stereo CD audio files which can be used with !CDBurn or !CDVDBurn. So there are two output spectra corresponding to the Left and Right channels of the stereo sound. As with previous applications, the results are saved into text files on your ramdisc.
1450 words
29th Nov 2007
Jim Lesurf