Time Patterns and Power Spectra
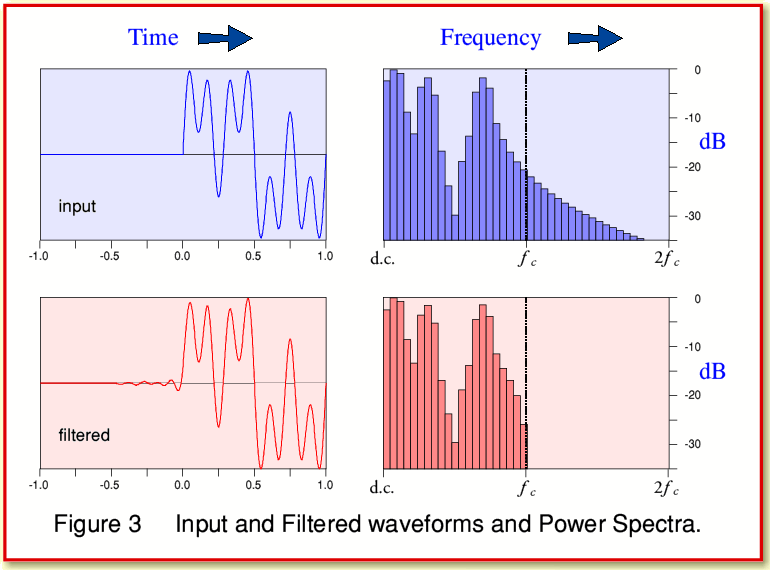
One of the most common ways to analyse and display signal patterns is in terms of their power spectra. If we compare the spectra of the input and output from the filter we get the results shown in Figure 3. Note that in order to compare these fairly I’ve chosen to re align the input and output in time so as to remove the overall time delay. Otherwise a simple delay would might look like a change and might mask any effect of the pre ringing.
When we examine the displayed results we find that – so far as the power spectra are concerned – the only real difference between the input and filtered patterns is that the filtered version has lost any details that were above the chosen frequency (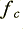 ) above which the filter blocks any components.
) above which the filter blocks any components.
It may seem odd that the spectra contain many more frequencies than just the three chosen for the waveform once it is ‘on’. This is a result of the way the waveform starts abruptly at a given instant. One of the consequences of a transient change like this is to create a burst of power over a range of frequencies that don’t then all persist during a sustained note. However, the traditional view would be that if all the frequencies above 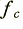 are too high to be audible, then there is no audible change in the power spectrum, and the filter should not produce an audible change.
are too high to be audible, then there is no audible change in the power spectrum, and the filter should not produce an audible change.
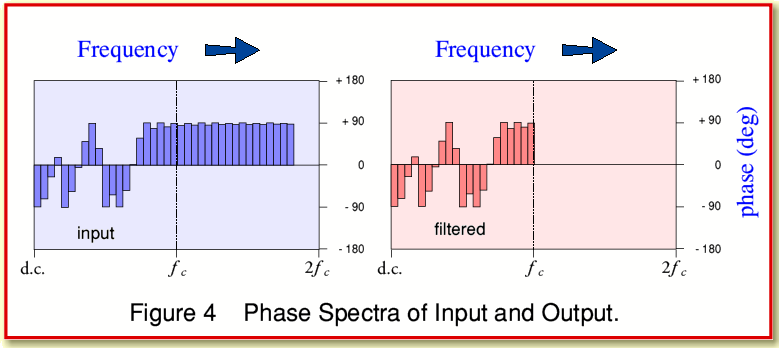
In fact, power spectra don’t tell the whole story. To determine all the details of a waveform we also need to know the relative phases (or relative time alignments) of the frequency components in a signal pattern. To see if this reveals anything, Figure 4 shows the phase spectra of the input and filtered waveforms.
Alas, once again, the only noticeable difference is the absence of the removed components above the filter’s cut-off frequency.
These results lead to the traditional view which may be summarised as: “Provided that we arrange for the chosen filter cut-off frequency value to be above 20kHz we should find that the spectra across the audible range are the same. Hence the pre ringing should not be audible.”
The snag with accepting this view is that human hearing does not work in the same manner as a Fourier Transform. Our ears don’t tend to divide the incoming signal into precisely defined ‘chunks’ with predetermined ‘start’ and ‘end’ instants and then perform a Fourier Transform to work out time-averaged values. Instead, human hearing employ a complex, non-linear, approach to detecting and recognising audible signals. Hence although the traditional view implies that the filtered waveform should sound indistinguishable from the input, human hearing might allow us to perceive a change.
Human Hearing
To test this possibility we can now apply some form of test based upon a knowledge of how human hearing works. This is quite a complex issue, and human hearing is far from being well understood. However we can try applying two relatively simple models. The first of these is an ‘old fashioned’ model which assumes that hearing is sensed using an array of linear bandpass filters inside the ears. The second takes into account the modern discovery that the sensors in the ears are non-linear, and have a sensitivity and effective bandwidth that vary with the applied signal levels.
Lets start with the simple linear model. This regards human hearing in terms of a series of bandpass resonant detectors. Each one sets out to detect any acoustic power in a particular narrow range of frequencies, and regularly report to the brain how the power in its frequency band varies as time progresses.
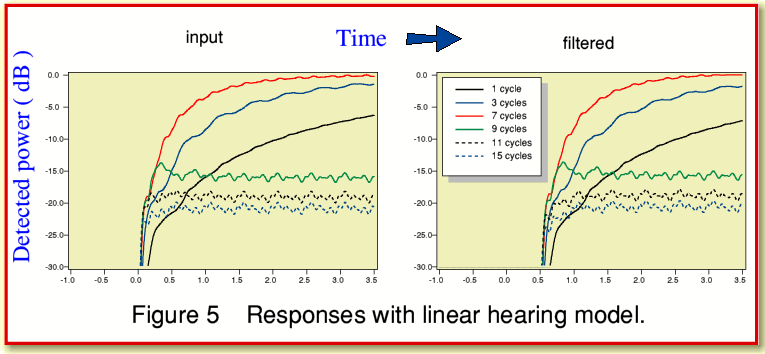
For the sake of illustration I decided to show the results from a set of resonant detectors having a bandwidth of approximately one tenth of an octave, centred on frequencies of 1, 3, 7, 9, 11, and 15 cycles per unit time. The values at 1, 3, and 7 cycles should respond to the frequencies that were explicitly built into our Burst137 waveform. The additional choices of 9, 11, and 15 cycles are intended to monitor the time variations of any power at these frequencies produced by the transient. If the digital filter were acting perfectly we would now expect that the responses of the 1, 3, 7, and 9 cycle hearing detectors would be same for both the original and filtered waveforms. We might also expect the 11 and 15 cycle detectors not to find anything at all in the filtered waveform. This is because our digital filter is designed to remove any power at frequencies above 10 cycles per unit time.
For the results displayed in Figure 5 I have not made any correction for the overall time delay produced by the filter. Hence the output (filtered) patterns are all delayed slightly as a result of the time-length chosen for the digital filter. The upper pair of graphs show the changes in power over a relatively long time period. The lower pair ‘zoom in’ to examine just a brief period centred on the nominal starting instant of the tone burst.
The first thing that becomes apparent when comparing the input and filtered results is that they show very similar shapes for the frequencies below the chosen cut-off value. There are some changes in the responses for the sensors at higher frequencies. These would be expected, since the filter is specifically designed to remove any such frequencies present in the signal. Despite this, the sensors for frequencies above the filter cut off do still respond to the filtered signal. This is because none of the filters are able to completely reject power at other frequencies. Hence the response of the high frequency sensors is mainly due their inability to completely ignore power at lower frequencies. In effect, the filters all ‘leak’ slightly. However if the conventional view is correct, human hearing may have no sensors for these high frequencies, so this should not matter. Comparing the patterns for the frequencies below filter cut off there are no obvious differences between the patterns of response for the input and filtered versions. This implies that – so far as this simple linear model is concerned – the filter does not seem to produce any audible effects.