Nonlinear Hearing model and filter pre-ringing
We can now examine the results of using a non-linear model of hearing. Here I’ve chosen to assume that the resonant sensors in the ear have a sensitivity and bandwidth that vary as the cube of the power level striking each sensor. This allows us to take into account the inherently nonlinear behaviour of the hearing system. Before going on to examine the results it is worth pointing out that I actually experimented with various power laws for this nonlinearity. In each case the results were broadly similar to those shown here. This finding was encouraging. It implies that – despite the differences between our model and more complex ones – the results may well be a fair description of the behaviour to be expected from the real hearing process.
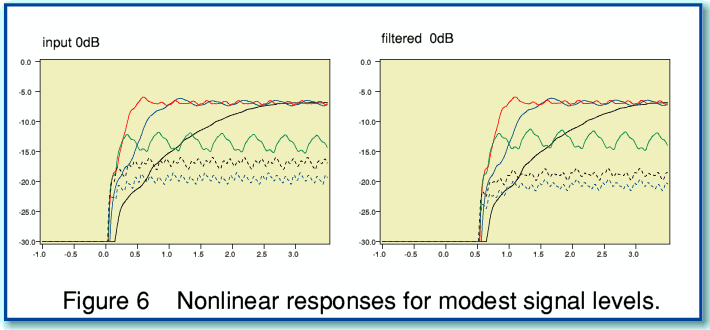
The response graphs shown in Figure 6 illustrate the results we get now for the original and filtered waveforms.
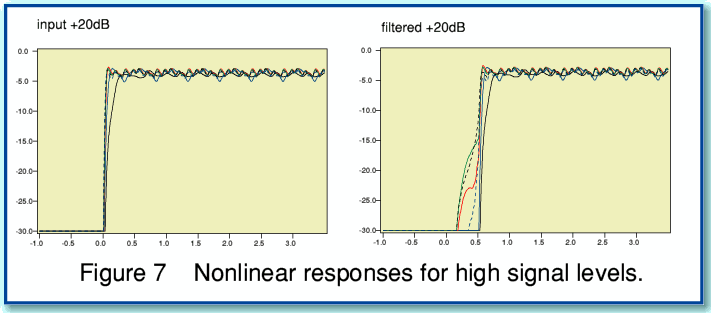
The response graphs shown in Figure 7 are for signal levels a factor of 100 times (+20dB) more powerful than those shown in Figure 6.
With linear systems the response patterns scale linearly with the input level. Hence if hearing was a linear process we would find that changing the input sound power level would displace the response patterns upwards or downwards in size, but would not alter any of the relative details or patterns. However with a nonlinear system the shapes of the response can be expected to be signal-level dependant. This can be seen to be the case if we compare Figures 6 and 7. The high power (Fig7) and moderate power (Fig 6) plots can be seen to differ in three ways.
- The high power graphs rise more quickly to a steady level. This is because the high powers reduces the response time of the sensors, so they react more swiftly to the start of the waveform.
- The size of the response for the higher powers is only slightly higher than for the lower powers. This is because the sensitivity is reduced by the higher power, so we don’t get a response that is 100 times larger despite having an input power that is increased by this amount.
- The relative levels detected by the sensors become ‘compressed’ by the high power. As a result all the sensors respond at much the same level. This is because the bandwidths which they accept are all widened by the high power. Hence each sensor now picks up more power from other frequencies which it would tend to reject at lower power levels.
All of the above arise from the properties of a nonlinear system. They serve to warn us that a linear model may not show us everything we’d need to know about the behaviour of a nonlinear system.
The most remarkable effect shown in Figure 7 is that we can see a distinct difference between the input and filtered response patterns during the pre ringing period. During this period, the sensors are responding to the filtered signal in a way that does not occur for the unfiltered waveform. This result is quite intriguing. The implication is that – as a result of the nature of human hearing – the pre ringing may perhaps have an audible effect which is not obvious when we apply traditional approaches like simple Fourier Transformation, or when we try to model hearing in a linear way.
The above result has to be treated with some care for various reasons. The non linear model employed here is a very simple one and omits many aspects of the complexity of human hearing. Hence the results should not be taken as ‘proof’ that we actually can and do hear pre ringing. However it does give some grounds for saying that it is, indeed, possible that pre ringing is audible. Hence pre ringing may well be a feature which is best avoided if we want to employ filters that are acoustically ‘harmless’.
Jim Lesurf
31st Mar 2004
References
1) Antialias filters and system transient response at high sample rates
P. G. Craven JAES Vol 52 (3) March 2004 pp 216-42
2) A suggested explanation for (some of) the audible differences between high sample rate and conventional sample rate audio material
Mike Storey www.dcsltd.co.uk/papers.htm
3) Upsampling upheaval, parts 1 and 2
K. Howard HFN March 2002 pp 76-9, and April 2002 pp 76-9
4) Now hear this
J. C. G. Lesurf HFN April 2004 (forgotten the page numbers!)
5) The power of hearing
T. Duke Physics World Vol 15 (5) May 2002 pp 29-33
6) Essential nonlinearities in hearing
V. M. Egufluz et. al. Phys. Rev. Let. Vol 84 (22) 29 May 2000 pp 5232-5
7) How well do we understand the cochlea?
R. Nobili, et. al. TINS Vol 21 (4) 1988 pp 159-67
8) The psychoacoustics of multichannel audio
J. R. Stuart available from Meridian Audio website.
9) Active travelling wave in the cochlea
T. Duke and F. Julicher Phys. Rev. Let. Vol 90 (15) 18 April 2003
10) A time-domain level-dependent auditory filter: the gammachirp
T. Irino and R. D. Patterson J. Acoust. Soc. Am. Vol 101 (1) Jan 1997 pp412-9